Roots of Unity

The $n$th roots of unity are the solutions to the equation

$$x^n-1=0$$

And the fundamental theorem of algebra tells us there are exactly $n$ solutions. Evidently 1 is always a solution and -1 is a solution only if $n$ is even. To find all the solutions, including the complex ones we do a bit of algebra to get

$$\begin{align*} x^n-1 & =0 \\ x^n & =1 \\ x & =\sqrt[n]{1} \\ \end{align*}$$

And to find the complex $n$th roots of 1 we need to think of a complex number $a+bi$ as a point on a plane where the real number $a$ is on the x-axis and the imaginary number $b$ is on the y-axis. Then we can represent a complex number in polar form $r(\cos \theta + i\sin \theta)$ where $r$ is the distance the point is from the origin and $\theta$ is the angle.

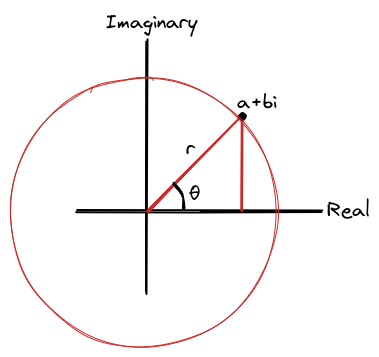
We actually have infinitely many ways to represent the complex number as

$$r(\cos(\theta + 2\pi k) + i\sin(\theta + 2\pi k)) \text{ for } k\in \mathbb{Z}$$

Because turning an angle by 360 degrees (or equivalently $2\pi$ radians) doesn't change it. Also, by Euler's formula

$$r(\cos(\theta + 2\pi k) + i\sin(\theta + 2\pi k))=re^{i(\theta+2\pi k)}$$

And expressing a complex number as a power of $e$ makes it really easy to take the $n$th root of a complex number as we just represent it in polar form and raise it to the 1/$n$th power

$$(re^{i(\theta + 2\pi k)})^{1/n}=r^{1/n}e^{i(\theta + 2\pi k)/n} \text{ for } k=0,1,2,\dotsc,n-1$$

Finding the $n$th root of unity becomes

$$\begin{align*} x^n-1 & =0 \\ x & =\sqrt[n]{1} \\ & =\sqrt[n]{1e^{i0}} \\ & =1^{1/n}e^{i(0 + 2\pi k)/n} & \text{ for } k=0,1,2,\dotsc,n-1 \\ & =e^{i(2\pi k)/n} & \text{ for } k=0,1,2,\dotsc,n-1 \end{align*}$$

I made a demo below which finds the $n$th roots of unity. JavaScript doesn't have imaginary numbers, so to calculate $e^{i(2\pi k)/n}$ we need to use Euler's formula again and express it equivalently as $\cos(2\pi k / n) + i\sin(2\pi k / n)$ and evaluate that. The slider directly below this paragraph controls number of decimal points.